For the convenience of research, theoretical cryptographers use Security Parameter to quantify the security of a cryptographic scheme and thus perform security analysis of cryptographic protocols.
Before analyzing the security of a cryptographic protocol, it is necessary to set up a certain security model, which includes the assumption of the attacker’s computational power. Shannon’s Information Theory investigates the security of an attacker under the condition of having unlimited computational resources, which we call Information-theoretic security. It can be studied from a statistical point of view, and we quantify this security with Statistical Security Parameter.
In practice, we usually assume that the attacker’s computational resources are limited, and this security is weaker than information theoretic security, which we call Computational Security. It can be studied in terms of computational complexity, and we quantify this security by the Computational Security Parameter.
Computational Security Parameter
Entities with limited computational resources have probabilistic polynomial (PPT) computational power. In general, any entity, including the attacker, is a PPT. Algorithms with a complexity of PPT can be implemented efficiently, while algorithms with a complexity of exponential are difficult to implement. We generally believe that a cryptographic scheme needs to satisfy both efficiency and security:
- the complexity of the individual algorithms in the scheme is of polynomial order
- The complexity of the algorithms of the code-breaking scheme is of exponential order
For an algorithm, we measure its complexity in terms of input length; then for a cryptographic algorithm, we measure its complexity in terms of computing security parameters.
The computational security parameter $\kappa$ means that the algorithmic complexity of the cracking scheme is $O(2^{\kappa})$.
With the safety constants, we can then measure the efficiency and safety of the scheme:
- The complexity of the individual algorithms in the program is polynomially related to the computational safety parameter
- the complexity of the algorithms of the cracking scheme is exponentially related to the computational security parameter
We consider the computational security parameter as the input length of a cryptographic scheme. The input length for the symmetric encryption regime can be viewed as the key length and plaintext length; the input length for the symmetric signature regime (hash algorithm) can be viewed as the message length. As for the asymmetric encryption and signature regimes, the key and message space are generated by the Setup algorithm, and the input length can be regarded as the input to the Setup algorithm.
In symmetric cryptography, the security of the scheme depends on the secrecy of the key or message. In asymmetric cryptography, the security of the scheme generally depends on a hard problem. The degree of difficulty varies from one difficult problem to another. For example, the DDH problem is strictly simpler than the CDH problem. Computing security parameters as input lengths to asymmetric cryptographic regimes can be used to measure the difficulty of different difficult problems, i.e., the complexity of the algorithms to crack different difficult problems. A cryptographic protocol may have many different cryptographic schemes, and the security of this protocol can be measured in terms of the total computational security parameter (minimum computational complexity): take the smallest computational security parameter among all schemes.
How to determine the value of $\kappa$ when designing a cryptographic scheme? We can determine the optimal computational complexity for breaking a particular cryptographic scheme based on research progress, and use the exponent of this complexity as the computational security parameter for this cryptographic scheme.The Keylength maintained by BlueKrypt is updated annually with the recommendations of various authoritative organizations on key lengths.
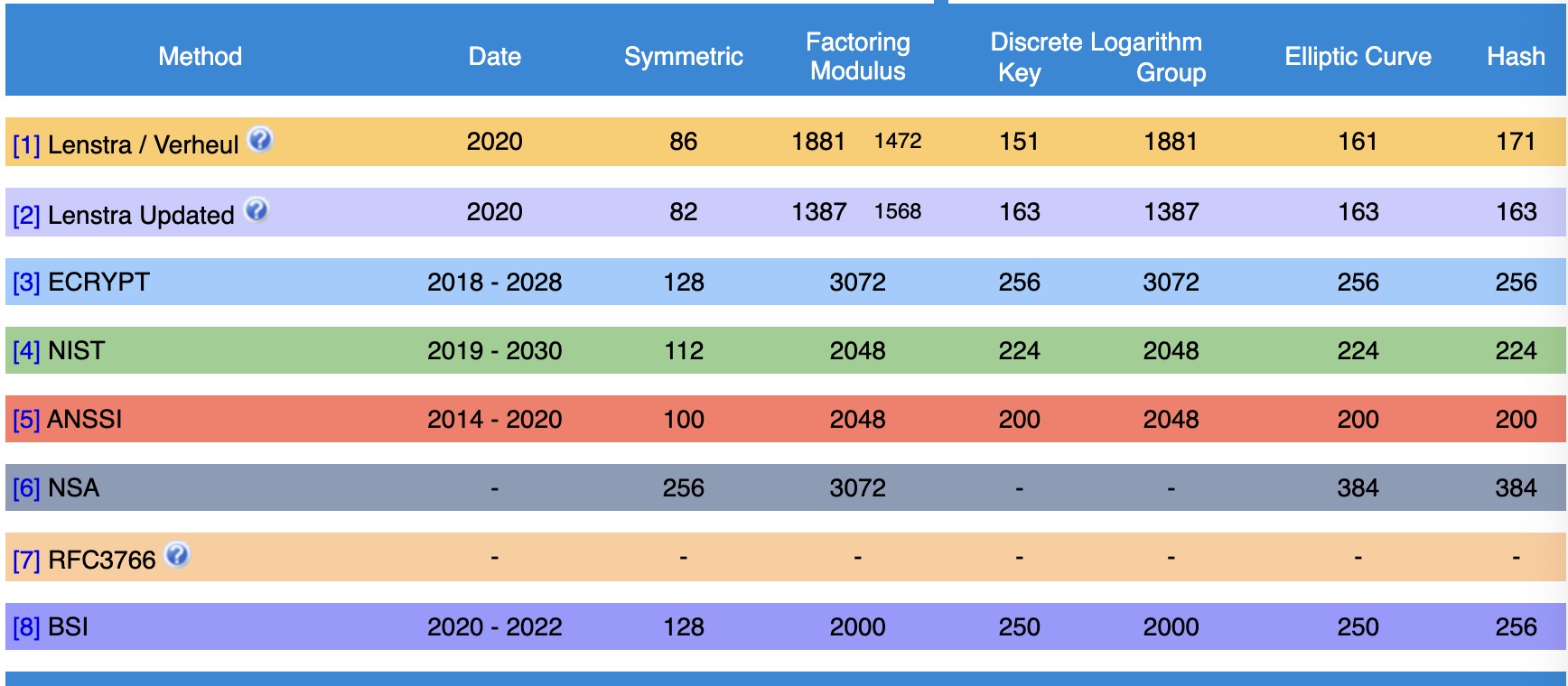
In practice we usually set $\kappa = 128$.
Statistical Security Parameter
Since the cipher scheme is public, the attacker can input a certain plaintext and study the distribution of the ciphertext under different randomness, a process called simulation. If there exists a certain plaintext and the secret value (the real plaintext) of the ciphertext distribution of the situation close to the other plaintext and the secret value of the ciphertext distribution of the difference is obvious, the attacker can easily guess that this plaintext is the secret value; if the secret value and the secret value and any other plaintext of the ciphertext distribution of the situation close to each other, then the attacker can not distinguish between which one is the real secret value.
We formalize this approximation using statistical theory:
When we say that two distributions are statistically close, we mean that the statistical distance between the distributions is a negligible function (negligeble function) 1. This function can be expressed in terms of a statistical safety parameter: $O(2^{-\sigma})$.
The statistical safety parameter is defined as follows:
The statistical security parameter $\sigma$ means that the probability of success of an attacker is at most $O(2^{-\sigma})$ even with unlimited computational resources.
The significance of the Statistical Security Parameter is to determine how statistically “close” any two input distributions in a cryptographic scheme are. The larger the statistical security parameter and the smaller the negligible function, the closer the two distributions are statistically. Therefore, the statistical security parameter can be used to measure the statistical security of different schemes.
In encryption schemes, a deeper understanding of security is that any information about the plaintext obtained from a given ciphertext can be obtained from a randomly sampled string of characters (of the same length as the ciphertext) that is independent of the plaintext. That is, a uniform distribution over a set of fixed-length strings is statistically close to a uniform distribution over the space of all possible ciphertexts.
In zero-knowledge protocols, statistical security parameters can be further subdivided into zero-knowledge statistical security parameters and reliable (Soundness) statistical security parameters. The former parameterizes the secret information leaked by Transcript, and the latter parameterizes the likelihood of a dishonest Prover convincing an honest Verifier that he knows a secret. Refer to the zero-knowledge proof section 2 for details.
In practice we usually set $\sigma$ = 40.