密码协议中的安全参数

为了研究的方便，理论密码学家用安全参数(Security Parameter)来量化一个密码方案的安全性，从而进行密码协议的安全性分析。

在分析密码协议的安全性前，需要先设置一定的安全模型¹，其中包括假设攻击者的计算能力。Shannon的信息论研究了攻击者在拥有无限制的计算资源条件下的安全，我们称之为信息论安全(Information-theoretic security)。它可以用统计学的观点来研究，我们用统计安全参数(statistical security parameter)来量化这种安全。

实践中，我们通常假设攻击者的计算资源是有限的，这种安全要弱于信息论安全，我们称之为计算安全(Computational Security)。它可以用计算复杂度的观点来研究，我们用计算安全参数(computational security parameter)来量化这种安全。

计算安全参数

计算资源有限的实体拥有概率多项式(PPT)的计算能力。一般来说，包括攻击者在内的任何实体都是PPT的。复杂度是PPT的算法可以被有效地实现，而复杂度是指数级的算法则很难被实现。我们一般认为，一个密码学方案需要满足高效性和安全性²：

• 方案中各个算法的复杂度是多项式级的
• 破解密码方案的算法复杂度是指数级的

对于一个算法，我们用输入长度来衡量它的复杂度；那么对于一个密码学算法，我们就用计算安全参数来衡量它的复杂度。

计算安全参数$\kappa$是指，破解方案的算法复杂度是$O(2^{\kappa})$。

通过安全常数，我们就可以度量方案的高效性和安全性了：

• 方案中各个算法的复杂度与计算安全参数呈多项式关系
• 破解方案的算法复杂度与计算安全参数呈指数级关系

我们将计算安全参数看作一个密码方案的输入长度。对称加密体制的输入长度可以看作密钥长度和明文长度；对称签名体制（哈希算法）的输入长度可以看作消息长度。而对于非对称加密体制和签名体制，密钥和消息空间是通过Setup算法生成的，输入长度可以看作是Setup算法的输入。

在对称密码学中，方案的安全性取决于密钥或消息的保密性。在非对称密码学中，方案的安全性一般依赖于一个困难问题。各个困难问题的困难度是不一样的。比如，DDH问题就严格比CDH问题简单。计算安全参数作为非对称密码体制的输入长度，可以用来衡量不同困难问题的困难度，即破解不同困难问题的算法复杂度。一个密码协议可能拥有很多不同的密码方案，这个协议的安全性可以用总的计算安全参数来度量（最小计算复杂度）：取所有方案中最小的计算安全参数。

在设计密码方案时，如何确定$\kappa$的值呢？我们可以根据研究进展，确定破解某一加密体制的最佳计算复杂度，把这个复杂度的指数作为这个加密体制的计算安全参数即可。BlueKrypt维护的Keylength每年都会更新各个权威组织对于密钥长度的建议。

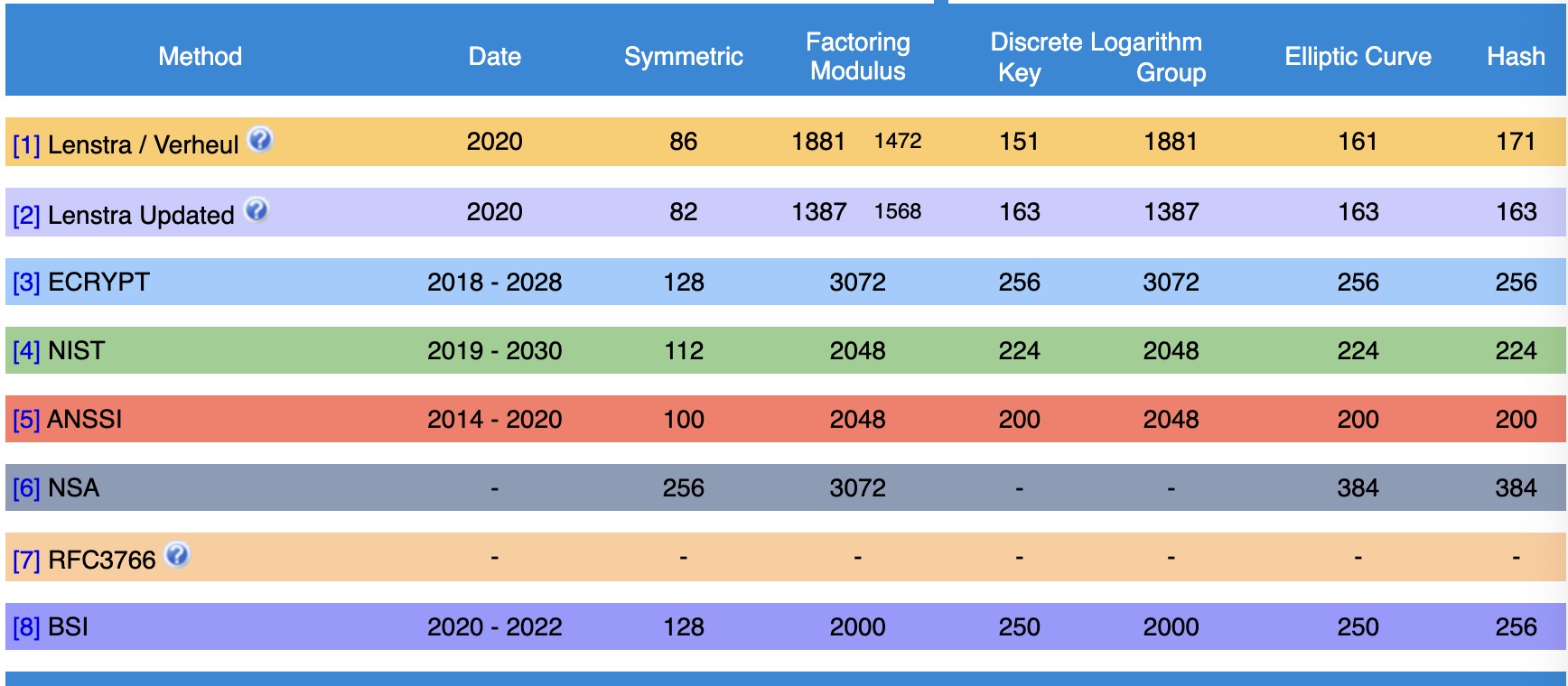
实践中我们通常设置$\kappa$ = 128。

统计安全参数

由于密码方案是公开的，攻击者可以输入某一明文，研究在不同随机性下密文分布情况，这个过程称为模拟。如果存在某一明文和秘密值（真正的明文）的密文分布情况接近，而其他明文和秘密值的密文分布差异明显，攻击者很容易猜测这一明文就是秘密值；如果秘密值和其他任意明文的密文分布都近似，那么攻击者就无法区分哪一个是真正的秘密值了。

我们使用统计学理论将这种近似形式化：

我们说两个分布在统计上是接近的，是说分布之间的统计距离是一个可忽略的函数(negligeble function)³。这个函数可以用统计安全参数来表示：$O(2^{-\sigma})$。

统计安全参数的定义如下：

统计安全参数$\sigma$是指，即使拥有无限制的计算资源，攻击者成功的概率最多只有$O(2^{-\sigma})$。

统计安全参数的意义是，判断密码方案中任意两个输入分布在统计上“有多接近”。统计安全参数越大，可忽略函数越小，两个分布的统计距离就越近。因此，统计安全参数可以用于衡量不同方案在统计上的安全性。

在加密方案中，对于安全性更为深层的一种理解是：从给定的密文中获得的任何关于明文的信息，都能从从独立于明文的（与密文长度相同）随机抽样字符串中获得。即一组固定长度的字符串上的均匀分布与所有可能的密文空间上的均匀分布在统计上是接近的。

在零知识协议中，统计安全参数可以进一步细分为零知识统计安全参数和可靠(Soundness)统计安全参数。前者参数化了Transcript泄露的秘密信息，后者参数化了一个不诚实的Prover说服一个诚实的Verfier他知道一个秘密的可能性。具体参考零知识证明部分⁴。

实践中我们通常设置$\sigma$ = 40。